Aufgabe A 2.1
In einem Skigebiet beträgt die Schneehöhe um 10.00 Uhr an einer Messstelle 150 cm.
Die momentane Änderungsrate dieser Schneehöhe wird beschrieben durch die Funktion s mit
s(t)=16e-0,5t-14e-t-2; 0≤t≤12
(t in Stunden nach 10.00 Uhr, s(t) in Zentimeter pro Stunde).a) Bestimmen Sie die maximale momentane Änderungsrate der Schneehöhe.
Ermitteln Sie den Zeitraum, in dem die momentane Änderungsrate der Schneehöhe größer als
2 cm pro Stunde ist.
Wie hoch liegt der Schnee um 12.00 Uhr?
(4 VP)
b) Bestimmen Sie einen integralfreien Funktionsterm der die Schneehöhe zum Zeitpunkt t beschreibt.Zu welchen Uhrzeiten beträgt die Schneehöhe 153 cm?
(3 VP)
c) Um 12.30 Uhr werden nun Schneekanonen in Betrieb genommen. Sie liefern konstant so viel Schnee, dass sich die momentane Änderungsrate der Schneehöhe an der Messstelle um 1 cm pro Stunde erhöht.Um wie viele Stunden verlängert sich durch diese Maßnahme der Zeitraum, in dem die Schneehöhe zunimmt?
Wie viele Zentimeter Schnee pro Stunde müssten die Schneekanonen ab 12.30 Uhr liefern, damit um 18 Uhr die Schneehöhe 160 cm betragen würde?
(4 VP)
Aufgabe A 2.2
Für jedes a>0 ist eine Funktion
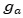gegeben durch
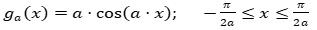
a) Bestimmen Sie für a=3 die Längen der beiden Diagonalen dieser Raute.
(2 VP)
b) Bestimmen Sie den Wert von a, für den die Raute ein Quadrat ist.(2 VP)